Thread
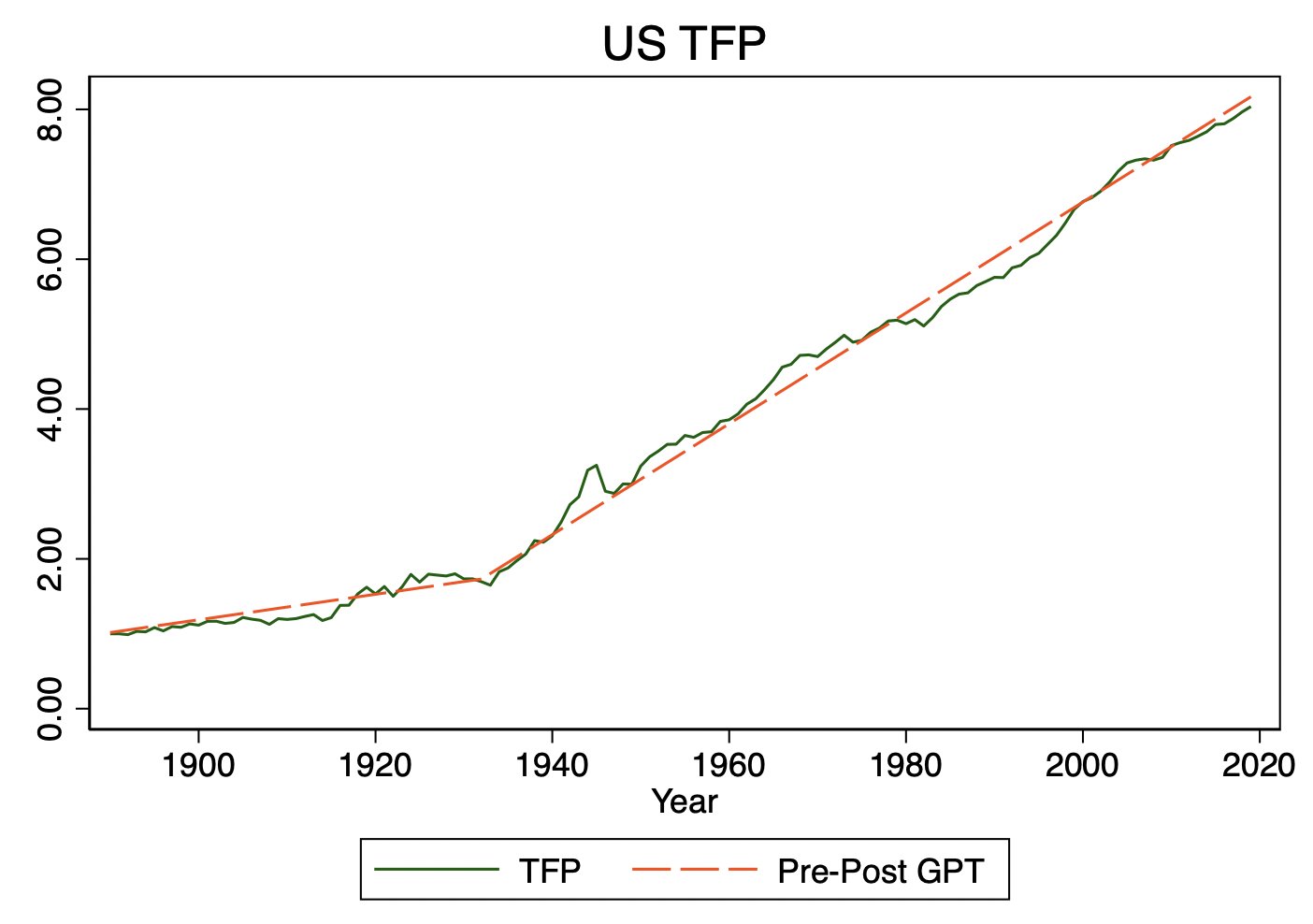
A few thoughts on this fascinating paper. The tl;dr of the paper is that national TFP (a common measure of "technology") behaves as if it grows at a constant linear rate, not exponentially, as is usually assumed. If TFP in 1947 = 1, increment it up by 0.0245/yr, not 1.45%/yr.
Some have pointed out that, if TFP grows linearly, then it's puzzling GDP per capita seems to grow exponentially. The paper has two answers to this.
First, GDP per capita depends on TFP + capital, so if economies invest in more and more capital, that generates a convex curve. The paper points out that better TFP makes capital more valuable, and so firms will invest in more capital as TFP rises, generating this kind of curve.
Second, the paper actually doesn't say TFP grows forever at a constant linear rate. There is a big trend break around 1933, where the TFP-time slope tilted upwards.
How to think about a "model" that allows arbitrary trend breaks like this? It kind of feels like adding epicycles, right?
I'm still mulling this over, but part of me views this as a feature, not a bug.
I'm still mulling this over, but part of me views this as a feature, not a bug.
Why should we expect the knowledge production function that underlies TFP to be a well-behaved exponential function in the first place? It's actually kind of surprising. Shouldn't technological progress exhibit a bit more weird and unpredictable randomness?
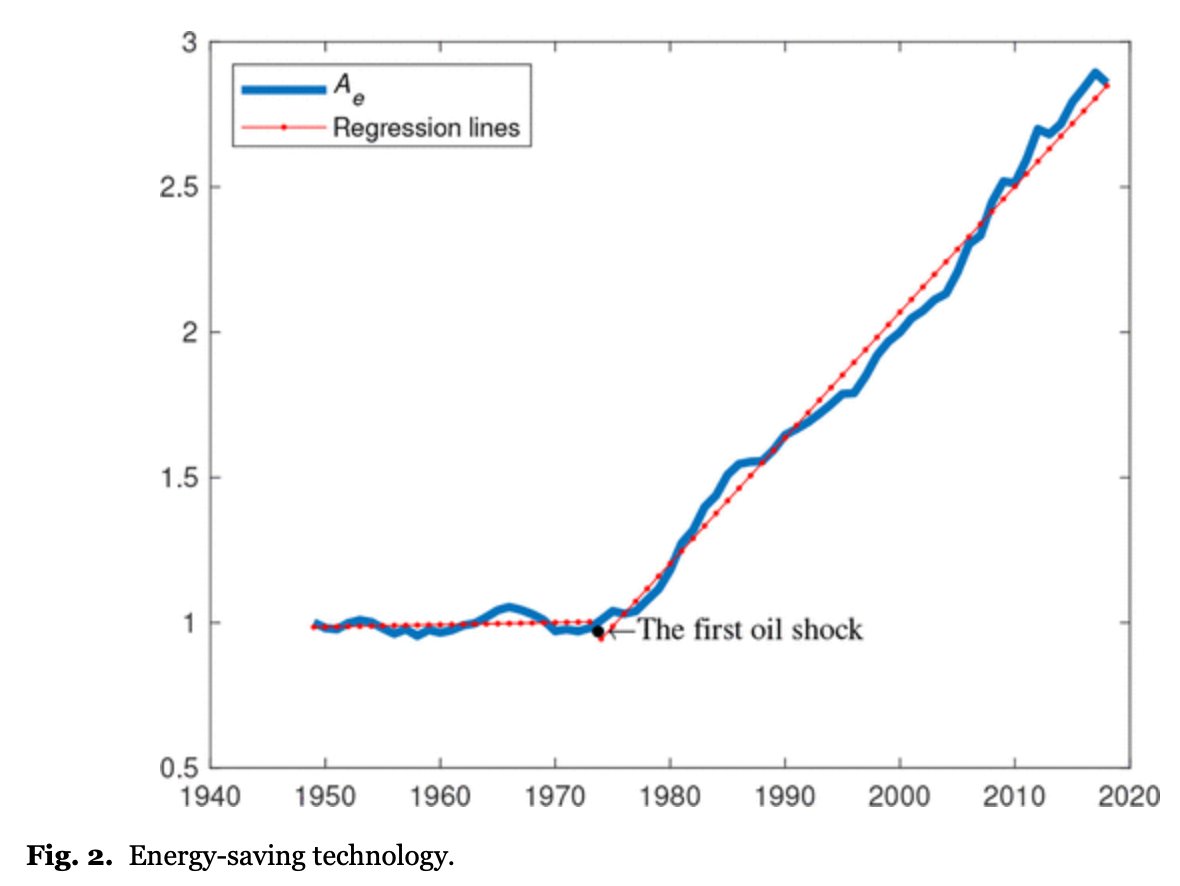
I can think of other examples for specific industries, of TFP-like measures exhibiting these kind of weird and ex-ante unpredictable trend-breaks. Left is US corn yields, right is an estimate of US energy productivity.
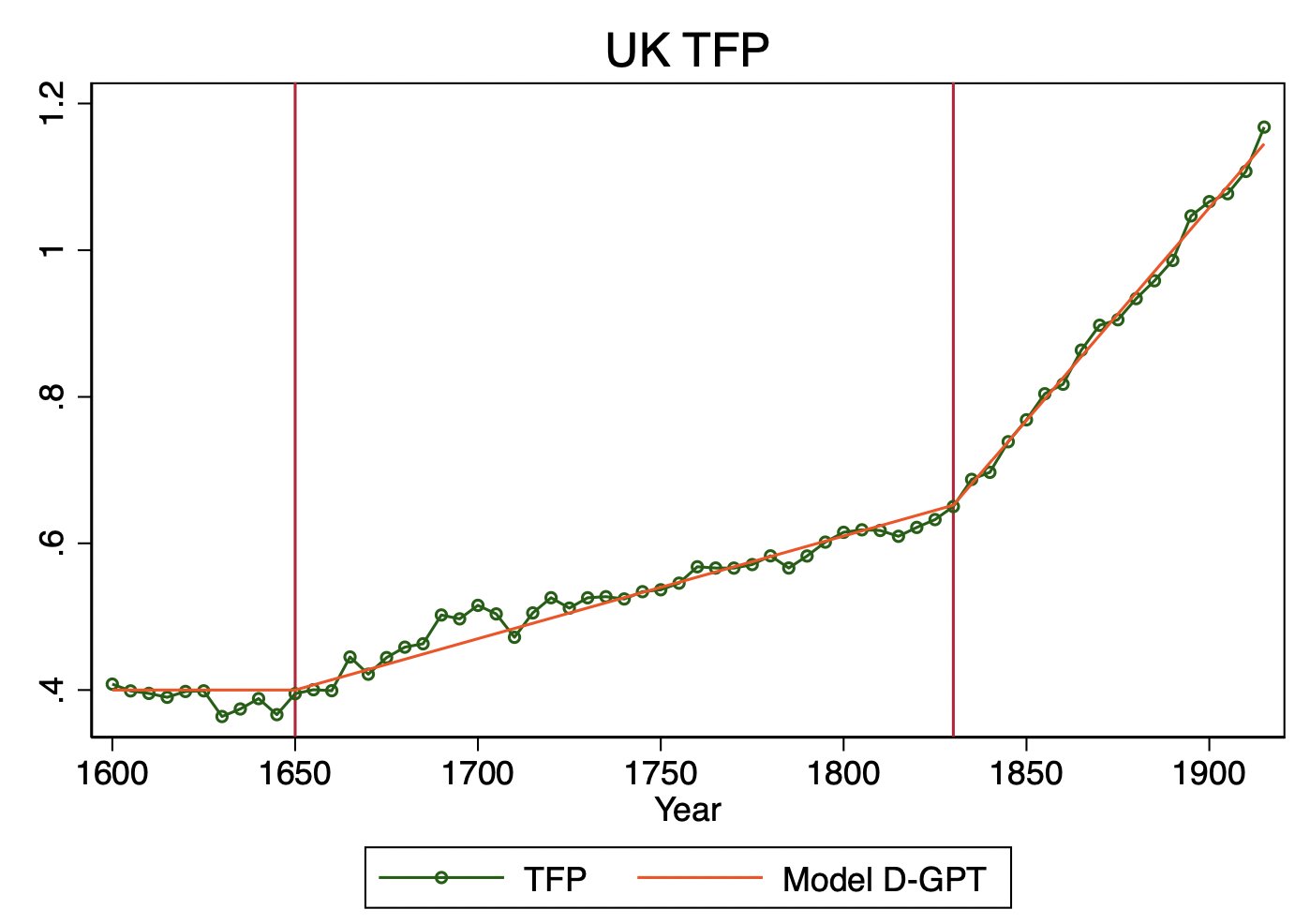
Moreover, the trend break in US TFP (which arises from statistical tests alone) does seem to line up reasonably well with narratives of when the US underwent a large-scale technological transformation. Similarly for a test of trend breaks in a proxy for UK TFP that goes way back.
That still leaves a bit of a mystery about why TFP exhibits any regularity at all though. Exponential TFP growth sort of made sense in the way that it allowed the stock of knowledge we have to impact the rate at which we produce new knowledge.
I'm not sure how this works with linear TFP growth, but I expect someone to show there are a variety of assumptions about how knowledge is produced that generate this kind of linear TFP growth. Will be interesting to see.
Lastly, if TFP growth really does grow at a linear rate, that sort of resolves the "puzzle" of slowing TFP growth. The assumption that the TFP growth rate should ever have been constant was just wrong-headed. We're actually in normal times, as far as TFP growth is concerned.
But that doesn't necessarily mean everything is going great. As Bloom et al pointed out, real R&D resources increased dramatically over the century, and the growth rate of TFP has not accelerated accordingly.
Source: www.aeaweb.org/articles?id=10.1257/aer.20180338
That's still true w/ linear TFP growth. A 20-fold rise in the effective number of researchers has not increased the annual increase of TFP over this period at all.
That's still true w/ linear TFP growth. A 20-fold rise in the effective number of researchers has not increased the annual increase of TFP over this period at all.
As for the future, this paper suggests that if we want future levels of GDP per capita that were implied by assumptions of constant exponential growth in TFP, then we need to engineer a trend break, not merely recover our former innovation mojo. Interesting food for thought.
Appendix. Sometimes you see arguments about how exponential growth for a long time leads to very weird outcomes, like this which points out that if 2% growth continues for 8200 years the economy would be 3x10^70 times bigger. www.cold-takes.com/this-cant-go-on/
Given 10^70 atoms in the galaxy, that’s a few global economies of value per atom!
Linear growth gives less bizarre outcomes. If TFP grew at 1.45%/yr for 8200 yrs, it reaches 1.8x10^51 current levels. If it grows at +0.0245/yr for 8200 yes, TFP reaches about 200x current levels.
Linear growth gives less bizarre outcomes. If TFP grew at 1.45%/yr for 8200 yrs, it reaches 1.8x10^51 current levels. If it grows at +0.0245/yr for 8200 yes, TFP reaches about 200x current levels.
Of course if trend breaks every century or two are possible then really, who knows!