Thread
Everyone should take a Probabilities course at least once.
The sad reality:
Most people know nothing about probabilities. This makes them gullible and easy to trick with numbers.
I have a story about a psychic. It got weird quickly:
The sad reality:
Most people know nothing about probabilities. This makes them gullible and easy to trick with numbers.
I have a story about a psychic. It got weird quickly:
Before telling you about the psychic, I partnered with @brilliantorg to discuss their Introduction to Probability course.
Here is what I love about them:
They break fundamentals into core building blocks organized in bite-sized lessons.
Courses at: brilliant.org/svpino.
Here is what I love about them:
They break fundamentals into core building blocks organized in bite-sized lessons.
Courses at: brilliant.org/svpino.
Alright, back to the psychic.
He sees things nobody else can.
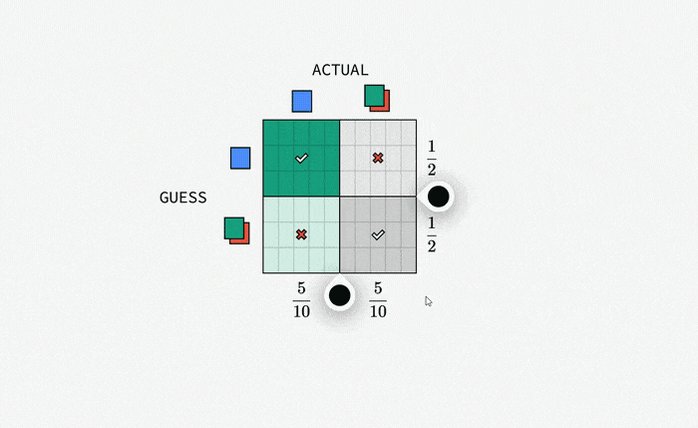
I showed him a stack of 10 colored cards and asked him to guess which color I would draw.
• 6 cards were blue.
• 3 cards were red.
• 1 card was green.
I drew a blue card, and the psychic got it right!
He sees things nobody else can.
I showed him a stack of 10 colored cards and asked him to guess which color I would draw.
• 6 cards were blue.
• 3 cards were red.
• 1 card was green.
I drew a blue card, and the psychic got it right!
The psychic knew there were 3 different colors, but I never told him the distribution.
I'm very skeptical. Was he guessing?
What's the probability of this person guessing and getting the correct answer?
I'm very skeptical. Was he guessing?
What's the probability of this person guessing and getting the correct answer?
There were 6 blue cards.
If the psychic was guessing, he had 1 out of 3 chances of guessing "blue." Therefore, he will likely get it correctly 6/10 x 1/3 = 1/5 = 20% of the time.
Not impressive, so I tried again.
If the psychic was guessing, he had 1 out of 3 chances of guessing "blue." Therefore, he will likely get it correctly 6/10 x 1/3 = 1/5 = 20% of the time.
Not impressive, so I tried again.
I put the blue card back in the stack, shuffled it, and drew a red card.
The psychic got it correctly again!
This time, 3 out of 10 cards were red. The psychic had 3/10 x 1/3 = 1/10 = 10% probability of guessing correctly.
I had to try again!
The psychic got it correctly again!
This time, 3 out of 10 cards were red. The psychic had 3/10 x 1/3 = 1/10 = 10% probability of guessing correctly.
I had to try again!
I drew two more cards: first, another red card, and finally, the green card.
The psychic answered correctly every time!
We know that the probability of guessing the red card is 10%, but the likelihood of guessing the green card is even smaller: 1/10 x 1/3 = 1/30 = 3.33%.
The psychic answered correctly every time!
We know that the probability of guessing the red card is 10%, but the likelihood of guessing the green card is even smaller: 1/10 x 1/3 = 1/30 = 3.33%.
But here is where things get weird:
What's the probability he guessed all four consecutive cards?
We can use the product rule to answer this:
1/5 x 1/10 x 1/10 x 1/30 = 1/15000 = 0.00007
That's almost impossible!
What's the probability he guessed all four consecutive cards?
We can use the product rule to answer this:
1/5 x 1/10 x 1/10 x 1/30 = 1/15000 = 0.00007
That's almost impossible!
This guy must have real powers, right?
Unless... Maybe there's something I didn't tell you:
This was not the only "psychic" I spoke to. I ran the same experiment with 100 people.
Unless... Maybe there's something I didn't tell you:
This was not the only "psychic" I spoke to. I ran the same experiment with 100 people.
How easy is it for any person to make one incorrect prediction?
The probability of somebody guessing correctly is 1/3. Guessing all four colors is (1/3)^4 = 1/81.
1 - 1/81 = 0.99
It's 99% likely a person makes one mistake.
But what if I ask 100 people?
The probability of somebody guessing correctly is 1/3. Guessing all four colors is (1/3)^4 = 1/81.
1 - 1/81 = 0.99
It's 99% likely a person makes one mistake.
But what if I ask 100 people?
We can use the product rule again: (1 - 1/81)^100.
The probability of every person making at least one mistake is much lower now: 29%.
See what's happening?
The probability of every person making at least one mistake is much lower now: 29%.
See what's happening?
I ran the experiment 100 times and found one person that guessed all four colors.
I then showed him to you and declared he is a psychic, and the numbers back me up.
This is "cherry picking."
A lot of what you read every day suffers from this. Don't let it happen to you.
I then showed him to you and declared he is a psychic, and the numbers back me up.
This is "cherry picking."
A lot of what you read every day suffers from this. Don't let it happen to you.
Don't forget to check @brilliantorg's Intro to Probabilities course!
This course is different.
The best part: it teaches Probabilities from first principles.
Click here for 30 free days + 20% off an annual membership: brilliant.org/svpino!
This course is different.
The best part: it teaches Probabilities from first principles.
Click here for 30 free days + 20% off an annual membership: brilliant.org/svpino!